Datenmanipulation ade (Teil 2) – Diagramme richtig interpretieren und manipulierte Daten enttarnen

In ihrem Beitrag ging es darum, wie man Diagramme richtig erstellt und welche Fallstricke es dabei zu beachten gilt. Ich möchte in meinem Blog-Beitrag an dieses Thema anknüpfen und Euch Tipps geben, die helfen, aus Diagrammen die richtigen Schlüsse zu ziehen.

Tipps zur richtigen Interpretation von Visualisierungen

Worauf muss man beim Lesen einer Visualisierung achten und wie erkennt man ob eine Darstellung manipuliert wurde? Folgende Beispiele geben Tipps, damit man in Zukunft noch erfolgreicher Dashboards interpretieren und Entscheidungen auf soliden Daten basieren kann.

Manipulierte Achsen in Diagrammen erkennen

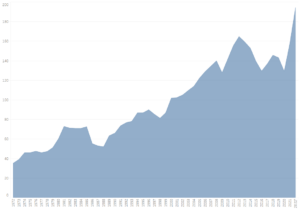
Als Beispiel folgendes Problem: Wir betrachten die Benzinpreise in Cent über die letzten Jahre in Deutschland. Wenn man sich das nicht manipulierte Diagramm ansieht steigen die Preise, wie erwartet, über die letzten Jahre. [5]

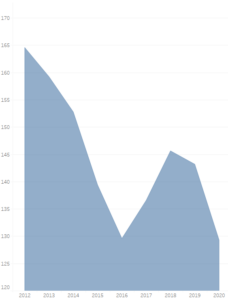
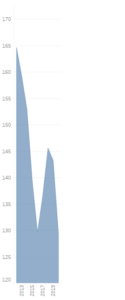
Nun die manipulierte Grafik:

Benzinpreis in Cent pro Jahr in Deutschland manipuliert, Quelle: Eigene Darstellung in Tableau

Was geübten Dashboard-Leser:innen sofort auffallen sollte, ist, dass die y-Achse nicht bei 0 beginnt. Dies ist häufig ein Zeichen dafür, dass die Grafik vom Ersteller verändert wurde. Dies kann auch aus Unwissenheit geschehen, da der Ersteller der Meinung ist, dass die Grafik so besser verständlich wird. In diesem Beispiel sorgt die Veränderung dafür, dass die Abnahme des Preises in den Jahren 2016 und 2020 sehr viel dramatischer aussehen, als in dem nicht manipulierten Diagramm. Dieser Eindruck wird durch die gastauchte x-Achse verstärkt. Daher ist es auch von Bedeutung, die Proportionen eines Diagramms zu hinterfragen.

Ein weiteres, was man beim Lesen eines Diagrammes beachten kann, ist die abgeschnittene x-Achse. In diesem Beispiel sollte man bemerken, dass nur wenige Jahre betrachtet werden, und besonders die aktuellsten fehlen. In diesem Fall ist es sinnvoll, weitere Nachforschungen anzustellen und auch die fehlenden Jahre zu betrachten. Dann sieht man schnell, dass die Preise nicht, wie hier dargestellt, stets gesunken sind, sondern einen deutlichen Anstieg gehabt haben.

Zusammenfassend ist es wichtig, die Beschriftungen der Achsen zu achten, um zu erkennen, ob die Achsen abgeschnitten wurden. Es ist auch sinnvoll, immer die Zahlen im Blick zu behalten sowie auf die Proportionen der Achsen zu achten. Wenn eine sehr gestaucht ist, sollte man misstrauisch werden. In unserem Beispiel ist dies sehr offensichtlich, da nur ungerade Jahre gezeigt werden. Die Geraden aus platzgründen aber nicht. Das deutet darauf hin, dass die Grafik manipuliert wurde.

Datengrundlage und die Störfaktoren

Störfaktoren sind Werte, die eigentlich nicht explizit in einer Statistik betrachtet werden, aber trotzdem das Ergebnis beeinflussen. Einer der häufigsten Störfaktoren ist das Alter der Personen, die getestet werden. Das möchte ich genauer betrachten. [6]

Schauen wir uns dieses Beispiel aus einem Video der Deutschen Gesellschaft für Internistische Intensivmedizin und Notfallmedizin an, bei dem sich die Erkenntnisse nach Berücksichtigung des Alters sogar umkehren. [3]

Wir betrachten hier die Todesrate von zwei Städten und sehen, dass Stadt A eine höhere Todesrate aufweist.

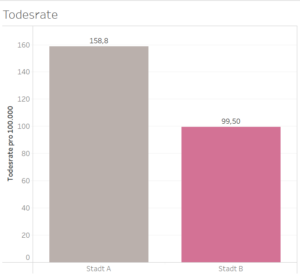
Wenn wir uns anhand der Grafik entscheiden müssten, in welcher der beiden Städte wir gerne leben würden, fällt die Entscheidung vermutlich auf Stadt B. Es ist jedoch wichtig, die Störfaktoren zu berücksichtigen, da das Alter auch einen Einfluss auf die Sterberate haben kann, da ältere Menschen in der Regel eher sterben als junge.

Daher beschließen wir, die Daten genauer unter die Lupe zu nehmen und die Sterberate nach Altersgruppen zu betrachten. Was werden wir entdecken?

Die rot markierten Zahlen sind die Todesraten pro 100.000 nach Altersgruppe. Hier fällt schnell auf, dass alle Todesraten nach Altersgruppe in Stadt B höher sind, als in Stadt A. Doch wie kommt das?

In Stadt A leben deutlich mehr ältere Menschen als Stadt B und diese sterben verhältnismäßig häufiger als die jüngeren Einwohner: innen. Dadurch wird die Gesamtsterblichkeitsrate so verzerrt, dass sie komplett gegensätzliche Erkenntnisse liefert, im Vergleich zur Sterberate nach Altersgruppen.

Als Leser: in sollte man sich immer überlegen, ob noch versteckte Faktoren, die das Ergebnis beeinflussen, in eine Statistik einbezogen wurden und diese dann separat betrachten. Leider gibt es keine Möglichkeit, nur anhand der Visualisierung zu testen, ob weitere Faktoren die Ergebnisse beeinflussen. Deshalb ist es wichtig sich weiter über das Thema zu informieren und die gesamte Datenlage zu betrachten.

Aus diesem Beispiel geht hervor, dass es wichtig ist, sich nicht nur auf die Visualisierung von Diagrammen zu verlassen, sondern auch die Datenlage zu betrachten. Dadurch können wir erkennen, ob es noch weitere Faktoren gibt, die die Darstellung beeinflussen können.

Anteil vs. Absolut

Eine weitere Quelle von Fehlinterpretationen ist der Unterschied zwischen Anteil und absoluten Werten. Folgende Grafik zeigt dies eindeutig:

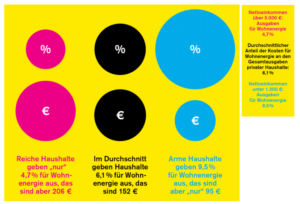
Wenn man auf die Größe der Kreise achtet verändert sich diese so stark, dass beim absoluten Anteil die armen Haushalte den kleinsten Betrag leisten, beim Durchschnittlichen Anteil in Prozent ist dies jedoch genau anderes herum.

Daher ist es wichtig die Zahlen zu beachten, um die korrekte Datenlage einfacher zu erkennen, als nur bei Betrachtung der Visualisierung.

Beispielsweise könnte man aus den anteiligen Zahlen schließen, dass reiche Haushalte weniger Energie verbrauchen als Haushalte mit mittlerem oder geringem Einkommen. Dies ist jedoch ein Trugschluss, der aufgedeckt wird, wenn man sich die absoluten Zahlen ansieht. [7]

Hier ist die Handlungsempfehlung klar: Die Zahlen anschauen. Und zwar sowohl die absoluten, als auch die anteiligen Zahlen. Dadurch können Leser:innen beide miteinander vergleichen und die richtigen Schlüsse daraus ziehen.

Vergleich von Daten: Korrelation Vs. Kausalität

Korrelation? Kausalität? Was war das nochmal? Unter Korrelation versteht man einen Zusammenhang zwischen zwei statistischen Werten, was aber nicht zwangsläufig bedeutet, dass diese sich beeinflussen. [1, 4]

Wenn das der Fall ist spricht man von Kausalität. Das bedeutet, dass dann wirklich einen Wert den anderen beeinflusst, also die Ursache für die Wirkung/das Verhalten des anderen Wertes darstellt. Beispielsweise gibt es starke Anzeichen dafür, dass Rauchen Lungenkrebs verursacht. Das wäre dann Kausalität. [1, 4]

Das wichtigste auf einen Blick: Korrelation bedeutet nicht, dass auch eine Kausalität vorliegt!

Korrelationen können nämlich rein zufällig auftreten. Eine Kennzahl, um die Stärke einer Korrelation zu messen ist der Korrelationskoeffizient, auch r-Wert genannt. Dieser nimmt Werte zwischen -1 und 1 an. Werte von -1 bis 0 lassen auf einen negativen Zusammenhang schließen. Werte von 0 bis 1 auf einen positiven Zusammenhang. Wenn der r-Wert sehr nahe an 0 ist, z.B. -0,02 oder 0,02 ist Vorsicht geboten, weil diese Korrelation zufällig auftreten könnte. [2]

Bei kleinen Stichproben sollte man ebenfalls vorsichtig sein, weil man bei diesen nicht davon ausgehen kann, dass sie repräsentativ sind.

Auch bei einem r-Wert nahe an 1 oder -1, sowie einer ausreichend großen Stichprobe, muss noch lange keine Kausalität vorliegen, wenn eine Korrelation erkennbar ist. Im folgenden Diagramm beträgt der r-Wert zum Beispiel 0.992558.

Beim Betrachten des Diagramms scheinen die Scheidungsrate in Maine und der pro Kopf Verbrauch an Margarine zusammenzuhängen. Verursacht also ein höherer Margarine-Verbrauch Scheidungen? Oder essen geschiedene Menschen mehr Margarine? Beides trifft wohl eher nicht zu- also ist diese Korrelation rein zufällig.

Oft kann man durch Logik ausschließen, dass eine Kausalität vorliegt. Beispielsweise wird bei unserem Diagramm nach kurzem Reflektieren klar, dass mehr Margarine nicht für mehr Scheidungen sorgt. Falls ein komisches Gefühl aufkommt, lohnt es sich außerdem die Quelle zu checken, ob diese vertrauenswürdig erscheint und ob dort weitere Infos zu den Daten und Diagrammen vorhanden sind.

Zusammenfassend ist es bei Korrelationen wichtig, dass bei diesen nicht zwangsläufig eine Kausalität vorliegt. Um dies zu beurteilen ist es sinnvoll weitere Recherchen anzustellen und sich nach Studien umzuschauen, die eine Kausalität nachweisen. Dies ergibt jedoch nur dann Sinn, wenn der dargestellte Sachverhalt auch schlüssig erscheint. Wenn wie hier Margarine Konsum mit Scheidungen in Verbindung gesetzt wird, kann man im Vorhinein davon ausgehen, dass das Diagramm nicht aus einer seriösen Quelle stammen kann.

Um gewollt, oder ungewollt manipulierte Diagramme zu erkennen und die richtigen Schlüsse daraus zu ziehen, genügt es nicht, nur schnell die Visualisierung zu betrachten. Es ist immer von Bedeutung die Zahlen und auch die Achsen in deiner Statistik zu beachten. Wenn etwas seltsam erscheint ist eine weitere Nachforschung zu dem dargestellten Thema ratsam.
Des Weiteren bietet es sich an zu hinterfragen, ob der dargestellte Sachverhalt auch sinnvoll erscheint. Dies ist vor Allem bei Korrelationen sehr wichtig, da diese häufig rein zufällig auftreten können.

Quelle:
[1] Blech, R. 2022. Korrelation und Kausalität • Unterscheidung und Beispiel. https://studyflix.de/statistik/korrelation-und-kausalitat-2216. Accessed 16 December 2022.
[2] Blech, R. 2022. Korrelationskoeffizient • Beispiele und Berechnung. https://studyflix.de/statistik/korrelationskoeffizient-2290. Accessed 16 December 2022.
[3] Deutsche Gesellschaft für Internistische Intensivmedizin und Notfallmedizin. 2016. Alter als Störfaktor (Confounder) in Studien. https://www.youtube.com/watch?v=lF-qkCceQZ8. Accessed 16 December 2022.
[4] Engelhardt, A. 2014. Korrelation und Kausalität | Crashkurs Statistik. https://www.crashkurs-statistik.de/korrelation-und-kausalitaet/. Accessed 16 December 2022.
[5] Münch, J. 2022. Datenmanipulation ade – Hintergrundinfos bieten und Diagramme hinterfragen (Teil 1) – Business -Software- und IT-Blog – Wir gestalten digitale Wertschöpfung. https://blog.doubleslash.de/datenmanipulation-ade-hintergrundinfos-bieten-und-diagramme-hinterfragen-teil-1/. Accessed 16 December 2022.
[6] Saemann, A. 2015. Störfaktor – DocCheck Flexikon. https://flexikon.doccheck.com/de/St%C3%B6rfaktor. Accessed 16 December 2022.
[7] Sauer, T. 2022. Dieser Text steigert dein Wissen um 200 %. https://www.fluter.de/statistiken-tricks. Accessed 19 December 2022.