Erkennung von Fahrbahnmarkierungen – Teil 1: Convolutional Neural Networks und wie sie funktionieren

Im ersten Teil werden zunächst Convolutional Neural Networks (kurz CNNs) betrachtet. Diese sind aus der Bildverarbeitung im Themenkomplex Deep Learning nicht mehr wegzudenken. Doch was zeichnet diese Netze aus und wie funktionieren sie? Genau das erfahren Sie in diesem Blogpost.

Der Aufbau eines Convolutional Neural Networks (CNN)

Ein wichtiger Unterschied zwischen einem klassischen neuronalen Netz und einem CNN besteht in der ersten Schicht, der sogenannten Input- oder Eingabeschicht. Während bei einem klassischen Netz der Input dieser Schicht als Vektor erwartet wird, ist ein CNN in der Lage, Input in Form einer Matrix zu verarbeiten. Gerade im Bereich der Bildverarbeitung ist dies ein großer Vorteil, da dadurch ein Bild als Matrix (Breite x Höhe x Farbkanäle) für die Eingabe verwendet werden kann. Ein Bild kann auch als Vektor dargestellt werden, indem die Pixel des Bildes hintereinander zu einem Vektor zusammengekettet werden. Dieses Vorgehen wird als „Flattening“ bezeichnet. Diese Form der Darstellung bringt das Problem mit sich, dass dadurch Objekte in einem Bild unabhängig ihrer Position nicht erkannt werden können. Wandert ein Objekt in einem Bild an eine andere Position, würde sich der Input in Vektorform stark unterscheiden. In der Matrixdarstellung wäre das Objekt weiterhin erkennbar, nur an seiner anderen Position. Anhang des Folgenden Beispiels soll kurz der Aufbau und die verschiedenen Schichten eines CNNs dargestellt werden:

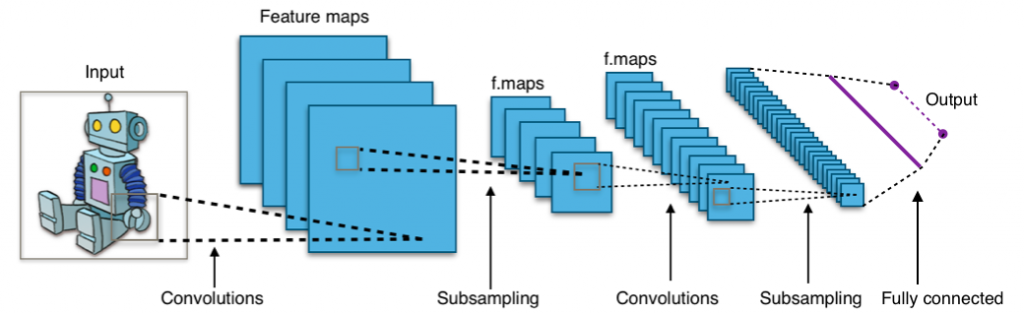
Layer im Überblick

• Convolutional Layer: Convolution wird meist mit „gefaltet“ übersetzt. Das bedeutet, dass der Input des CNNs zunächst eine Anzahl von Filter mit fester Pixelgröße (z.B. 2 x 2 oder 3 x 3) durchläuft. Diese Filter wandern von links nach rechts über das Bild (die Input Matrix) und springen in die nächste Zeile, wenn sie am rechten Rand angekommen sind. Diese „Wanderung“ lässt sich mit zwei Parametern steuern, dem sogenannten Padding und der Step Size (auch mit Stride bezeichnet). Mit dem Padding kann das Verhalten des Filters beim Erreichen des Randes gesteuert werden, indem beispielsweise der Rand der Matrix mit 0 Werten gefüllt wird. Die Step Size bestimmt, wie weit der Filter jeweils nach rechts wandert, also um wie viele Pixel dieser weiterwandert.

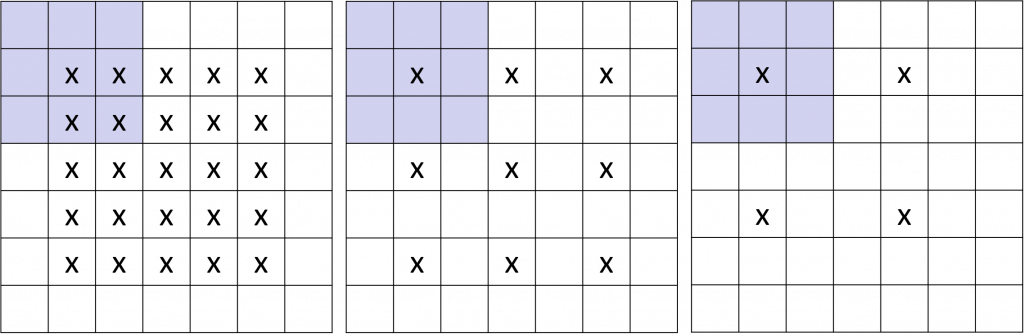
In dem obenstehenden Bild wir der Stride Parameter verdeutlicht. Die mit „x“ markierten Felder stellen die jeweiligen Mittelpunkte des Filters bei der Wanderung dar. Im ersten Bild ist der Stride mit 1 konfiguriert, also der Mittelpunkt wandert jeweils einen Pixel nach rechts. In Bild 2 wird der Stride auf 2 erhöht, woraufhin nur jeder zweite Pixel als neuer Mittelpunkt genutzt wird. Im letzten Bild beträgt der Wert des Stride Parameters 3. Die Filter besitzen für jeden Pixel in ihrem Sichtfenster ein festes Gewicht. Aus den Pixelwerten des Bildes im Sichtfenster und dem Gewicht des jeweiligen Pixels des Filters im Sichtfenster wird insgesamt eine Ergebnismatrix für diesen Filter in dem bestimmten Sichtbereich errechnet.

• Pooling (Subsampling) Layer: Ein Pooling Layer kann auch als Subsampling (oder auch Unterabtastung) gesehen werden. Ziel ist dabei, die Matrizen zu verkleinern, um ein einfacheres (weil kleineres) Modell zu erhalten. Beispiele hierfür wären ein Max- oder ein Average-Pooling. Hier ein kurzes anschauliches Bild des Max-Poolings:

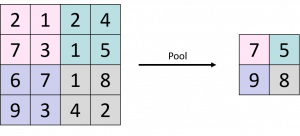
• Wie dabei zu sehen ist, wird in einem bestimmten Bereich (z.B. 2×2) hierbei immer der höchste Wert verwendet. Insgesamt führt das im konkreten Beispiel zu einer Halbierung der Matrixgröße. Beim Average-Pooling wird in einem Bereich (z.B. 2×2) jeweils der Mittelwert berechnet und dieser für die verkleinerte Matrix verwendet.
• Fully Connected Layer: Der Fully Connected Layer stellt eine „normale“ neuronale Netzstruktur dar. Hierbei sind alle Neuronen mit allen Inputs und allen Outputs verbunden. Um die bisherigen Werte in Matrixform in diese Schicht einbringen zu können, müssen die Matrizen zunächst durch „Flattening“ auf Vektorform gebracht werden. Diese letzte Schicht des Netzes besitzt, beispielsweise im Falle einer Objektklassifikation, genauso viele Ausgabeneuronen wie Ausgabeklassen vorhanden sind.

Hyperparameter

Als Hyperparameter werden Parameter bezeichnet, die entweder die Netzwerkstruktur determinieren oder festlegen wie das Netzwerk trainiert wird. Hyperparameter werden vor dem Training bestimmt und werden im Vergleich zu den Gewichten und Bias nicht optimiert. Hyperparameter können die Performance eines Netzwerkes stark beeinflussen. Ihre perfekten Werte können pauschal leider nicht angegeben werden und müssen meist durch viele Experimente ermittelt werden. Zu den wichtigsten Hyperparametern gehören:

• Tiefe des Netzes (=Anzahl der Schichten): Die Tiefe eines Netzwerkes kann sehr einfach modifiziert werden. Tiefere Netzwerke können zwar komplexere Strukturen erlernen, neigen jedoch zu Overfitting. Overfitting kann einfach auch als „auswendig Lernen“ gesehen werden. Dabei kann es vorkommen, dass das Modell perfekte Ergebnisse auf den Trainingsdaten erzielt, da es diese auswendig gelernt hat. Auf bisher unbekannten Daten (z.B. den Testdaten) erzielt das Modell, aufgrund der Spezialisierung auf die Trainingsdaten, unter Umständen schlechte Ergebnisse. Ein Beispiel wird in folgendem Diagramm dargestellt. Darin wird die Verlustfunktion (siehe nächster Abschnitt) dargestellt. Diese sollte im Idealfall immer weiter sinken (siehe Trainingsdaten, orange Linie). Aufgrund des Overfittings performt das hier gezeigte Modell jedoch auf den Testdaten (blaue Linie) sehr schlecht und die Verlustfunktion steigt ab etwa Trainingsdurchlauf 30 wieder an.

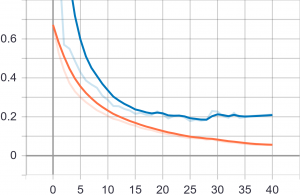
• Lernrate: Die Lernrate bestimmt, wie schnell ein Modell ein bestimmtes Problem erlernen kann. Sehr hohe Lernraten können jedoch zu einem instabilen Trainingsprozess führen.
• Anzahl an Epochen: Eine Epoche beschreibt den Durchlauf aller Input-Daten, die Messung des Fehlers sowie die Backward Propagation zur erneuten Anpassung der Gewichte. Ein zu langes Training kann in einer zu starken Fokussierung der Trainingsdaten (Overfitting) und einer schlechteren Generalisierungsfähigkeit münden.
• Batch Größe: Um weniger Speicherplatz zu benötigen und schneller trainieren zu können, werden die Daten, die durch das Netzwerk propagieren, in Batches aufgeteilt. Es gilt jedoch: Je kleiner die Batch Größe, desto weniger akkurat wird die Schätzung des Gradienten. Ein Batch bezeichnet die Anzahl an Trainingsdaten, die während des Trainings durch das Netz propagiert werden. Dabei werden am Ende des Durchlaufs eines Batchs die Gewichte und der Bias aktualisiert.

Verlustfunktion

Damit ein neurales Netz den generierten Output bewerten kann, gibt es die Verlustfunktion. Sie wird zur Berechnung des Fehlers zwischen realen und vorhergesagten Werten verwendet. Das Ziel ist es, den berechneten Fehler zu minimieren. Dazu werden die Gewichte und der Bias des Netzes angepasst. Gewichte, welche in klassischen neuronalen Netzen die Verbindungen zwischen den einzelnen Neuronen gewichten, spiegeln sich in CNNs als Filter wieder. Beispiele für eine solche Verlustfunktion (oder „Loss-Function“) sind Binary-Cross-Entropy bzw. allgemein die Cross-Entropy.

Metriken

Um die Performance eines neuronalen Netzes bewerten zu können, werden Metriken auf dem Modell unbekannten Daten berechnet. Die intuitivste Metrik ist die Genauigkeit („Accurarcy“). Diese gibt den Prozentwert der als richtig erkannten Klassen an. Leider ist diese Metrik in vielen Fällen nicht für die Performancemessung geeignet, beispielsweise bei ungleich verteilen Klassen.
Deutlich wird das an einem klassischen Beispiel: Die Klassifizierung, ob es sich bei Bildern um ein Katzen- oder ein Hundebild handelt. Nehmen wir an, 99% der Bilder zeigen Hunde und lediglich 1% zeigt Katzen. Würde unser Modell jedes Bild als Hundebild klassifizieren, würde es damit eine Genauigkeit von 99% erzielen. Das sieht nach einem grandiosen Wert aus, jedoch könnten wir so unseren eigentlichen Anwendungsfall, in welchem wir auch Katzen erkennen möchten, nicht umsetzen.

Andere Metriken nutzen eine sogenannte Confusion-Matrix. Im folgenden Bild wird eine vereinfachte Matrix dargestellt mit den beiden Klassen „Hund“ und „Katze“. Natürlich gibt es solche Matrizen auch für mehr als zwei Klassen.

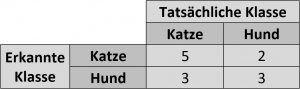
In einer solchen Matrix gibt es folgende Einträge:

• True Positives / True Negatives: Stimmt die Klasse, welche vom Modell ermittelt wurde mit der wirklichen Klasse überein, spricht man von True Positives und/oder True Negatives (je nachdem, was als positiv und negativ gekennzeichnet ist). In der Matrix stellen die Einträge links oben und rechts unten die Werte für True Positives (kurz TP) und True Negatives (kurz TN) dar.
• False Positives / False Negatives: Als False Positives (kurz FP) werden in unserem Beispiel diejenigen Fälle bezeichnet, bei denen ein eigentliches Hundebild als Katzenbild klassifiziert wurde. Umgekehrt bezeichnen False Negative (kurz FN) diejenigen Ergebnisse, bei denen ein eigentliches Katzenbild als Hundebild klassifiziert wurde.

Aus diesen Kennzahlen lassen sich diverse Metriken berechnen. Eine weit verbreitete hierfür ist der sogenannte F-Score, oder auch F1-Score. Dieser berücksichtigt neben den TP und TN auch die beiden anderen Kennzahlen FN und FP.

Fazit

Die Nutzung von Convolutional Neural Networks (kurz CNNs) ist aus dem Bereich der Bildverarbeitung mit neuronalen Netzen nicht mehr wegzudenken. Die nötigen Grundlagen, um diese Netze besser zu verstehen, wurden im Blogbeitrag erläutert. Es wurde der Aufbau eines solchen Netzes aus den Schichten Convolutional Layer, Pooling Layer und Fully Connected Layer gezeigt. Dieser Aufbau ermöglicht es, CNNs Objekte in Bildern unabhängig ihrer Position als Ganzes zu erkennen. Weiter wurden die Thematiken Verlustfunktion und Hyperparameter erläutert, die sowohl Einfluss auf die Trainingsdauer, als auch auf das Trainingsergebnis haben. Abschließend wurden im Beitrag noch die Kennzahlen True Positives, True Negatives, False Positives und False Negatives untersucht. Mithilfe dieser Kennzahlen lassen sich Metriken zur Bewertung des Modells berechnen um die Performance bewerten zu können. Teil 2 der Blogserie beschäftigt sich mit Bildsegmentierung und wie CNNs in diesem Bereich verwendet werden.

Co-Autor: Nils Boerner

Mehr rundum das autonome Fahren gibt’s hier

Mehr zu künstlicher Intelligenz erfahren

Quellen

1 https://www.deeplearningbook.org/contents/convnets.html

2 https://cs231n.github.io/convolutional-networks/