Was sind künstliche Neuronale Netze: Ein praktischer Einstieg

In den letzten Jahren wurden mit Hilfe von künstlichen neuronalen Netzen bisher unmöglich geglaubte Fortschritte in Bereichen des maschinellen Lernens erreicht. Ein Beispiel hierfür ist Alphabets künstliche Spielintelligenz für das vor allem in Asien sehr beliebte und hochkomplexe Spiel Go. Das „AlphaGo“ genannte Programm nutzt ebenfalls neuronale Netze und besiegte 2016 zum ersten Mal einen menschlichen Spieler des höchsten Rangs.

Quelle: https://upload.wikimedia.org/wikipedia/commons/2/2a/FloorGoban.JPG[1]

Künstliche Neuronale Netze (englisch: Artificial Neural Networks) entlehnen ihren Namen biologischen neuronalen Netzen, wie sie zum Beispiel im menschlichen Nervensystem und Gehirn zu finden sind. Doch während unser Gehirn wohl auch in Zukunft noch viele Geheimnisse bergen wird, ist das Grundprinzip künstlicher neuronaler Netze überraschend einfach und zugänglich.
Ich möchte in diesem Beitrag die Grundprinzipien und die praktische Nutzung neuronaler Netze anhand eines eingängigen Beispiels zeigen. Dazu stellen wir uns vor, wir möchten über Gesten mit einem elektronischen Gerät kommunizieren und eine Zahl zwischen eins und fünf eingeben. Dazu nutzen wir eine der folgenden Handgesten:

Unser Programm soll nun in der Lage sein, aus dem Foto unserer Handgeste die korrekte Zahl abzuleiten. Wir möchten also Bilder in fünf Kategorien von eins bis fünf sortieren. Diese Problemstellung wird als Klassifizierung (engl.: classification) bezeichnet. Wer direkt die Beispielimplentation ausprobieren möchte, kann dies mit unserer Demoanwendung tun.

Das Grundprinzip künstlicher Neuronaler Netze

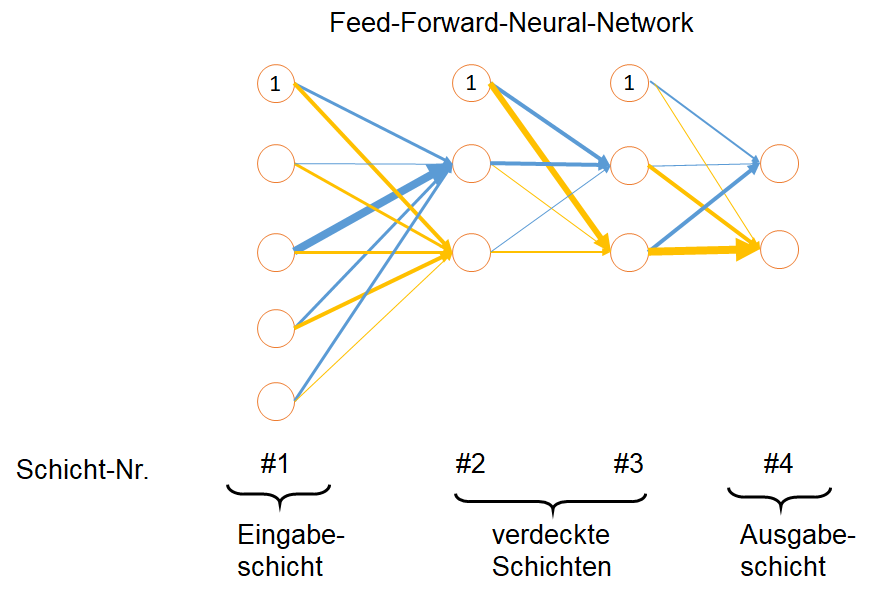
Die Grundidee künstlicher neuronaler Netze basiert auf einem aus der Biologie inspirierten Prinzip: aus für sich sehr einfach gehaltenen Elementen lassen sich im Verbund beliebig komplexe Konstrukte abbilden. Unser Gehirn besteht in dieser Modellvorstellung aus einer Vielzahl vernetzter Neuronen, die jeweils einen von zwei Zuständen annehmen: aktiviert oder nicht aktiviert, bzw. sendet das Neuron ein Signal, oder bleibt stumm. Ein Neuron wird aktiviert, wenn ausreichend viele der mit ihm verbundenen Neuronen ihrerseits aktiviert sind. Verallgemeinern wir das Modell, kann ein Neuron nicht nur zwei Zustände annehmen, sondern beliebige Werte zwischen eins und null. Schauen wir uns dazu ein einfaches künstliches neuronales Netz an:

Das Schaubild wird von links nach rechts gelesen. Jeder Kreis zeigt ein Neuron, welche in Schichten angeordnet sind (hier nummeriert von eins bis vier). Die äußerste linke Schicht wird als Eingabeschicht bezeichnet (engl.: input layer). Nutzen wir als Eingangsdaten z.B. Graustufenbilder, so entspricht jeder Pixel in einem Testbild einem Neuron, das konstant den entsprechend Grauwert dieses Pixels ausgibt. Alle Neuronen der Eingabeschicht sind in unserem Beispielbild nun jeweils mit jedem Neuron der nächsten Ebene verbunden, der sogenannten verdeckten Schicht (engl.: hidden layers). Die Neuronen der ersten verdeckten Schicht erhalten als Eingabe eine gewichtete Summe der Neuronen der Eingangsschicht, was im Schaubild mittels unterschiedlich dicker Pfeile visualisiert ist. Dadurch werden die Signale der Neuronen in jeder Schicht unterschiedlich stark an die Neuronen der nächsten Schicht weitergegeben.

Schauen wir uns nun ein beliebiges Neuron der verdeckten Schichten an (Schichten #2 und #3). Gemäß der Pfeildicke der eingehenden Neuronen wird im Zielneuron eine gewichtete Summe gebildet. Anhand dieser Signalstärke wird nun entschieden, ob das Neuron aktiviert werden soll, oder nicht. Dabei kann ein Neuron nicht nur aktiviert oder deaktiviert sein, sondern die Neuronenaktivität wird auf einer Skala von null bis eins abgebildet. Hierzu wird eine sogenannte Aktivierungsfunktion eingesetzt, die aus der gewichteten Summe der Eingangsneuronen die Neuronenaktivität berechnet.

Die Klassifikation eines Bildes erfolgt schließlich in der Ausgabeschicht. In unserem Handgestenbeispiel möchten wir die Bilder in fünf unterschiedliche Klassen unterteilen – eine Klasse für jede Handgeste. Daher benötigen wir fünf Ausgabeneuronen. Jedes Ausgabeneuron gibt dabei die Wahrscheinlichkeit an, dass das Bild der entsprechenden Klasse angehört. Das Ausgabeneuron mit der höchsten Wahrscheinlichkeit wird für die Klassifikation des Bildes genutzt.

Bevor wir ein neuronales Netz nutzen können um Bilder zu klassifizieren, müssen nun insbesondere die Pfeildicken ermittelt werden (die sogenannten Gewichte), die darüber entscheiden, wie sehr ein Neuron ein anderes beeinflusst. Für ein vollkommen neues neuronales Netz werden die Gewichte zunächst zufällig gewählt.

Um die Gewichte zu ermitteln nutzen wir bereits vorhandene Daten. Für unser Gestenerkennungsbeispiel verwenden wir als Datengrundlage das Sign Language Digits Dataset, das von Schülern der türkischen Ankara Ayrancı Anadolu High School erstellt wurde und unter der Apache-2.0-Lizenz über Github zur freien Verfügung steht. Der Datensatz umfasst Gesten von null bis neun und besitzt für jede der Kategorien knapp 200 Bilder. Diese Datenmenge ist recht klein für ein künstliches neuronales Netz, reicht aber für unsere kleine Einführung aus. Die folgende Abbildung zeigt beispielhaft fünf Bilder aus dem Datensatz, welche die Geste „Drei“ darstellen:

Wir beschränken uns auf die Handgesten von eins bis fünf, da diese Gesten jedem geläufig sind und sich der Aufwand für eigene Testfotos dadurch in Grenzen hält. Zusätzlich setzen wir entsprechend den Ausgangsdaten voraus, dass die Handgeste vor einem einfarbigen Hintergrund fotografiert wird, dass das Foto bereits zugeschnitten wurde und die rechte Hand genutzt wird. Alle Voraussetzungen stellen keine generelle Einschränkung neuronaler Netze dar, sondern sind lediglich dem kleinen Datensatz und unserer beschränkten Entwicklungszeit geschuldet.

Um nun die Gewichte der einzelnen Neuronen zu erhalten, teilen wir den Datensatz in sogenannte Trainings- und Testdaten auf. Für jedes Bild aus einem Trainingsdatensatz wird die Klassifikation des neuronalen Netzes mit der korrekten Klassifikation verglichen. Korrekte Vorhersagen werden mathematisch belohnt und falsche Vorhersagen werden bestraft, was mathematisch über eine sogenannte Zielwertfunktion ausgedrückt wird. Nun wird ein Optimierungsalgorithmus genutzt, um diese Zielwertfunktion zu minimieren und so einen Satz an Gewichten zu finden, welche die Trainingsdaten möglichst gut vorhersagen können.
Nachdem ein ausreichend guter Satz an Gewichten gefunden wurde, wird mittels des Testdatensatzes überprüft, ob das neuronale Netz auch mit Daten gute Ergebnisse erzielt, für die es nicht explizit optimiert wurde.

Technologien zur Implementierung von neuronalen Netzen

Zur Implementierung eines neuronalen Netzwerks steht uns grundsätzlich eine Vielzahl von Technologien zur Verfügung. Von der kompletten eigenen Implementierung in einer beliebigen Programmiersprache, bis hin zu hoch-spezialisierten, vorgefertigten Lösungen mit unterschiedlichem Abstraktionslevel. Für unser Einführungsbeispiel wählen wir als Programmiersprache Python. Python ist eine beliebte Programmiersprache im wissenschaftlichen und Datenanalysekontext, wodurch ein recht breites, frei verfügbares Ökosystem an Bibliotheken zur Datenverarbeitung und -modellierung existiert. Als Interpretersprache erlaubt Python einen interaktiven Zugang zur Datenquelle, wodurch eine sehr effiziente Datenexplorations- und Modellierungsphase möglich ist. Wir nutzen die Bibliotheken scikit-image (zur Bildverarbeitung), numpy (für effiziente mathematische Operationen), sowie matplotlib (zur Erstellung von Plots) und das Projekt jupyter (zur Bereitstellung besserer interaktiver Werkzeuge).

Für das eigentliche neuronale Netzwerk greifen wir auf Tensorflow zurück. Tensorflow ist ein von Google entwickeltes Machine-Learning-Framework das effiziente, parallelisierte Berechnungen erlaubt und das eine Schnittstelle für Python zur Verfügung stellt. Grundlage für die effiziente Berechnung mit Tensorflow ist die Erstellung eines Berechnungsgraphen. Tensorflow kann daraufhin die notwendigen Berechnungen optimal ausführen und so hochparallelisierte Rechnungen auf Grafikkarten durchführen. Für diese Einführung greifen wir auf die High-Level-API von Tensorflow zurück, die bereits parametrisierte, vorgefertigte Schätzer (sogenannte Estimator) zur Verfügung stellt.

Für diese Einführung verwenden wir den DNNClassifier-Schätzer, also einen Deep-Neural-Network-Schätzer. Dieser erlaubt es uns, das zuvor skizzierte sehr einfache neuronale Netz mit einer von uns vorgegebenen Anzahl verdeckter Schichten und Anzahl von Neuronen pro verdeckter Schicht anzugeben. Alle verdeckten Schichten besitzen dabei zunächst die gleiche Anzahl von Neuronen ¹.

Datenaufbereitung für neuronale Netze

Bevor wir das neuronale Netz mit Daten füttern können, müssen wir diese zunächst aufbereiten. Unser Trainingsdatensatz ist bereits sehr gut aufbereitet, so dass die vorhandenen Bilder lediglich eingeladen und verkleinert werden müssen.
Die gleichen Operationen werden auf Bilder angewandt, die vom Nutzer bereitgestellt werden. Um unabhängiger von der Hintergrundfarbe des Bildes und den Lichtverhältnissen zu werden, konvertieren wir zusätzlich alle Bilder in einen anderen Farbraum. Anstatt den Rot-Grün-Blau (RGB) Farbraums, nutzen wir den HSV-Farbraum, der Farben in Farbwert, Farbsättigung und Hellwert beschreibt.

Quelle: https://de.wikipedia.org/wiki/Datei:HSV_cone.png [2]

Modellierung und Nutzung der Daten für neuronale Netze

Die aufbereiteten Bilder werden genutzt, um das Tensorflowmodell zu trainieren und optimierte Neuronengewichte zu finden. Um die Qualität des Modells zu testen wird der Testdatensatz genutzt. Das Modell erhält ein Testbild als Input. Die erkannte Handgeste des Modells wird dann mit der korrekten Antwort verglichen. Ein gutes Modell sollte einen Großteil der Testbilder korrekt klassifizieren, dabei aber gleichzeitig auch eine gute Erkennungsrate mit einem dritten Validierungsdatensatz zeigen.
Möchte ein Nutzer ein neues Bild klassifizieren lassen, so werden alle Transformationen zunächst auf das Bild angewandt und dann an das neuronale Netzwerk übergeben. Als Ergebnis zeigt uns das Modell, mit welcher Wahrscheinlichkeit es das Bild den einzelnen Handgesten von eins bis fünf zuordnet.

Künstliche neuronale Netze können aus sehr einfachen Bauteilen sehr komplexe mathematische Funktionen erzeugen. Schon mit einem vergleichsweise einfachen neuronalen Netzwerk lassen sich manchmal sehenswerte Ergebnisse erzeugen. Das zeigen wir mit unserer Demoanwendung, die Handgesten von eins bis fünf auf Bildern erkennt.

Mit Machine Learning beschäftigen wir uns auch auf unserem Expertentalk am 21.2.2019 in München mehr erfahren

¹ Das resultierende Modell hat allerdings nicht unbedingt in jeder Schicht die gleiche Anzahl an Neuronen. Um Overfitting zu verhindern, nutzen wir eine Regularisierungstechnik (Dropout), die zufällig ausgewählte Neuronen aus dem Netz entfernt.

Quellen

[1] https://upload.wikimedia.org/wikipedia/commons/2/2a/FloorGoban.JPG

[2] Representation of colors in the HSV system. Image created by (3ucky(3all using Borland Delphi 2006, Adobe Photoshop 9.0. Not modified. CC BY-SA 3.0